平台：win10 x64 +VS 2015专业版 +opencv-2.4.11 + gtk_-bundle_2.24.10_win32
主要参考：1.代码：RobHess的SIFT源码：SIFT+KD树+BBF算法+RANSAC算法
2.书：王永明 王贵锦 《图像局部不变性特征与描述》
RobHess的SIFT源码分析：xform.h和xform.c文件
这两个文件中实现了RANSAC算法(RANdom SAmple Consensus 随机抽样一致)。
RANSAC算法可用来筛选两个图像间的SIFT特征匹配并计算变换矩阵。
请在看这个之前先看完以下内容前五个：
SIFT四步骤和特征匹配及筛选：
问题及解答：
（1）问题描述：利用RANSAC算法筛选SIFT特征匹配的主要流程是什么？
答：
(1) 从样本集中随机抽选一个RANSAC样本，即4个匹配点对
(2) 根据这4个匹配点对计算变换矩阵M
(3) 根据样本集，变换矩阵M，和误差度量函数计算满足当前变换矩阵的一致集consensus，并返回一致集中元素个数
(4) 根据当前一致集中元素个数判断是否最优(最大)一致集，若是则更新当前最优一致集
(5) 更新当前错误概率p，若p仍大于允许的最小错误概率则重复(1)至(4)继续迭代，直到当前错误概率p小于最小错误概率
RANSAC算法的迭代终止条件是当前错误概率p小于允许的最小错误概率p_badxform，一般传入的值为0.01，即要求正确率达到99%
当前错误概率p的计算公式为：p=( 1 - in_fracm)^k，
其中in_frac是当前最优一致集中元素(内点)个数占样本总数的百分比，表征了当前最优一致集的优劣；
m是计算变换矩阵需要的最小特征点对个数，是固定值，一般是4；k是迭代次数。
所以，内点所占比例in_frac越大，错误概率越小；迭代次数k越大，错误概率越小，用来保证收敛。
（2）问题描述：RobHess的源码如何实现RANSAC，大概思路是这样的？
答：（2.1）代码及说明：——match.c的main函数里
/*下面的观察看看RANSAC功能如何运作
注意上面的这一行：
feat1[i].fwd_match = nbrs[0];
对于RANSAC功能起作用很重要。
*/
//计算变换参数，利用RANSAC算法筛选匹配点,计算变换矩阵H
{
CvMat* H; //RANSAC算法求出的变换矩阵
IplImage* xformed; //xformed临时拼接图，即只将图2变换后的图
//无论img1和img2的上下顺序，H永远是将feat1中的特征点变换为其匹配点，即将img1中的点变换为img2中的对应点
H = ransac_xform( feat1, n1, FEATURE_FWD_MATCH, lsq_homog, 4, 0.01,
homog_xfer_err, 3.0, NULL, NULL );
//feat1：特征点数组；n1：特征点个数；FEATURE_FWD_MATCH：特征点类型，三者之一；lsq_homog：函数指针（2.2.5）；4：在lsq_homog中计算变换矩阵需要最小特征点对个数；0.01：允许的错误概率，当前计算出的错误概率小于0.01时停止；homog_xfer_err：函数指针（2.2.6.1）；3.0：容错度（此范围内认为是内点）
//若能成功计算出变换矩阵，即两幅图中有共同区域
if( H )
{
//为拼接结果图xformed分配空间,高度为图2高度
xformed = cvCreateImage( cvGetSize( img2 ), IPL_DEPTH_8U, 3 );
//用变换矩阵H对右图img1做投影变换(变换后会有坐标右移)，结果放到xformed中
cvWarpPerspective( img1, xformed, H,
CV_INTER_LINEAR + CV_WARP_FILL_OUTLIERS,
cvScalarAll( 0 ) );
cvNamedWindow( "Xformed", 1 ); //创建窗口
cvShowImage( "Xformed", xformed ); //显示临时图,即只将图2变换后的图
cvWaitKey( 0 );
cvReleaseImage( &xformed );
cvReleaseMat( &H ); //释放变换矩阵H
}
}
（2.2）ransac_xform代码及说明：
答：
/*利用RANSAC算法进行特征点筛选，计算出最佳匹配的变换矩阵
参数：
features：特征点数组，只有当mtype类型的匹配点存在时才被用来进行单应性计算
n：特征点个数
mtype：决定使用每个特征点的哪个匹配域进行变换矩阵的计算，应该是FEATURE_MDL_MATCH，
FEATURE_BCK_MATCH，FEATURE_MDL_MATCH中的一个。若是FEATURE_MDL_MATCH，
对应的匹配点对坐标是每个特征点的img_pt域和其匹配点的mdl_pt域，
否则，对应的匹配点对是每个特征点的img_pt域和其匹配点的img_pt域。
xform_fn：函数指针，指向根据输入的点对进行变换矩阵计算的函数，一般传入lsq_homog()函数
m：在函数xform_fn中计算变换矩阵需要的最小特征点对个数
p_badxform：允许的错误概率，即允许RANSAC算法计算出的变换矩阵错误的概率，当前计算出的模型的错误概率小于p_badxform时迭代停止
err_fn：函数指针，对于给定的变换矩阵，计算推定的匹配点对之间的变换误差，一般传入homog_xfer_err()函数
err_tol：容错度，对于给定的变换矩阵，在此范围内的点对被认为是内点
inliers：输出参数，指针数组，指向计算出的最终的内点集合，若为空，表示没计算出符合要求的一致集
此数组的内存将在本函数中被分配，使用完后必须在调用出释放：free(*inliers)
n_in：输出参数，最终计算出的内点的数目
返回值：RANSAC算法计算出的变换矩阵，若为空，表示出错或无法计算出可接受矩阵
CvMat* ransac_xform( struct feature* features, int n, int mtype,
ransac_xform_fn xform_fn, int m, double p_badxform,
ransac_err_fn err_fn, double err_tol,
struct feature*** inliers, int* n_in )
{
//matched：所有具有mtype类型匹配点的特征点的数组，也就是样本集
//sample：单个样本，即4个特征点的数组
//consensus：当前一致集；
//consensus_max：当前最大一致集(即当前的最好结果的一致集)
struct feature** matched, ** sample, ** consensus, ** consensus_max = NULL;
struct ransac_data* rdata;//每个特征点的feature_data域的ransac数据指针
CvPoint2D64f* pts, * mpts;//每个样本对应的两个坐标数组：特征点坐标数组pts和匹配点坐标数组mpts
CvMat* M = NULL;//当前变换矩阵
//p：当前计算出的模型的错误概率，当p小于p_badxform时迭代停止
//in_frac：内点数目占样本总数目的百分比
double p, in_frac = RANSAC_INLIER_FRAC_EST;
//nm：输入的特征点数组中具有mtype类型匹配点的特征点个数
//in：当前一致集中元素个数
//in_min：一致集中元素个数允许的最小值，保证RANSAC最终计算出的转换矩阵错误的概率小于p_badxform所需的最小内点数目
//in_max：当前最优一致集(最大一致集)中元素的个数
//k：迭代次数，与计算当前模型的错误概率有关
int i, nm, in, in_min, in_max = 0, k = 0;
//找到特征点数组features中所有具有mtype类型匹配点的特征点，放到matched数组(样本集)中，返回值nm是matched数组的元素个数
nm = get_matched_features( features, n, mtype, &matched );
//若找到的具有匹配点的特征点个数小于计算变换矩阵需要的最小特征点对个数，出错
if( nm < m )
{ //出错处理，特征点对个数不足
fprintf( stderr, "Warning: not enough matches to compute xform, %s" \
" line %d\n", __FILE__, __LINE__ );
goto end;
}
srand( time(NULL) );//初始化随机数生成器
//计算保证RANSAC最终计算出的转换矩阵错误的概率小于p_badxform所需的最小内点数目
in_min = calc_min_inliers( nm, m, RANSAC_PROB_BAD_SUPP, p_badxform );
//当前计算出的模型的错误概率,内点所占比例in_frac越大，错误概率越小；迭代次数k越大，错误概率越小
p = pow( 1.0 - pow( in_frac, m ), k );
i = 0;
//当前错误概率大于输入的允许错误概率p_badxform，继续迭代
while( p > p_badxform )
{
//从样本集matched中随机抽选一个RANSAC样本(即一个4个特征点的数组)，放到样本变量sample中
sample = draw_ransac_sample( matched, nm, m );
//从样本中获取特征点和其对应匹配点的二维坐标，分别放到输出参数pts和mpts中
extract_corresp_pts( sample, m, mtype, &pts, &mpts );
//调用参数中传入的函数xform_fn，计算将m个点的数组pts变换为mpts的矩阵，返回变换矩阵给M
M = xform_fn( pts, mpts, m );//一般传入lsq_homog()函数
if( ! M )//出错判断
goto iteration_end;
//给定特征点集，变换矩阵，误差函数，计算出当前一致集consensus，返回一致集中元素个数给in
in = find_consensus( matched, nm, mtype, M, err_fn, err_tol, &consensus);
//若当前一致集大于历史最优一致集，即当前一致集为最优，则更新最优一致集consensus_max
if( in > in_max )
{
if( consensus_max )//若之前有最优值，释放其空间
free( consensus_max );
consensus_max = consensus;//更新最优一致集
in_max = in;//更新最优一致集中元素个数
in_frac = (double)in_max / nm;//最优一致集中元素个数占样本总个数的百分比
}
else//若当前一致集小于历史最优一致集，释放当前一致集
free( consensus );
cvReleaseMat( &M );
iteration_end:
release_mem( pts, mpts, sample );
p = pow( 1.0 - pow( in_frac, m ), ++k );//更新当前错误概率
}
//根据最优一致集计算最终的变换矩阵
//若最优一致集中元素个数大于最低标准，即符合要求
if( in_max >= in_min )
{
//从最优一致集中获取特征点和其对应匹配点的二维坐标，分别放到输出参数pts和mpts中
extract_corresp_pts( consensus_max, in_max, mtype, &pts, &mpts );
//调用参数中传入的函数xform_fn，计算将in_max个点的数组pts变换为mpts的矩阵，返回变换矩阵给M
M = xform_fn( pts, mpts, in_max );
/***********下面会再进行一次迭代**********/
//根据变换矩阵M从样本集matched中计算出一致集consensus，返回一致集中元素个数给in
in = find_consensus( matched, nm, mtype, M, err_fn, err_tol, &consensus);
cvReleaseMat( &M );
release_mem( pts, mpts, consensus_max );
//从一致集中获取特征点和其对应匹配点的二维坐标，分别放到输出参数pts和mpts中
extract_corresp_pts( consensus, in, mtype, &pts, &mpts );
//调用参数中传入的函数xform_fn，计算将in个点的数组pts变换为mpts的矩阵，返回变换矩阵给M
M = xform_fn( pts, mpts, in );
if( inliers )
{
*inliers = consensus;//将最优一致集赋值给输出参数：inliers，即内点集合
consensus = NULL;
}
if( n_in )
*n_in = in;//将最优一致集中元素个数赋值给输出参数：n_in，即内点个数
release_mem( pts, mpts, consensus );
}
else if( consensus_max )
{ //没有计算出符合要求的一致集
if( inliers )
*inliers = NULL;
if( n_in )
*n_in = 0;
free( consensus_max );
}
//RANSAC算法结束：恢复特征点中被更改的数据域feature_data，并返回变换矩阵M
end:
for( i = 0; i < nm; i++ )
{
//利用宏feat_ransac_data来提取matched[i]中的feature_data成员并转换为ransac_data格式的指针
rdata = feat_ransac_data( matched[i] );
//恢复feature_data成员的以前的值
matched[i]->feature_data = rdata->orig_feat_data;
free( rdata );//释放内存
}
free( matched );
return M;//返回求出的变换矩阵M
}
（2.2.1）get_matched_features代码及说明：
答：
/*找到所有具有mtype类型匹配点的特征点，将他们的指针存储在matched数组中，
并初始化matched数组中每个特征点的feature_data域为ransac_data类型的数据指针参数：features：特征点数组n：特征点个数mtype：匹配类型matched：输出参数，含有mtype类型匹配点的特征点的指针数组返回值：matched数组中特征点的个数static int get_matched_features( struct feature* features, int n, int mtype, struct feature*** matched ){ struct feature** _matched;//输出数组，具有mtype类型匹配点的特征点指针数组 struct ransac_data* rdata;//ransac_data类型数据指针 int i, m = 0; _matched = calloc( n, sizeof( struct feature* ) ); //遍历输入的特征点数组 for( i = 0; i < n; i++ ){ //找第i个特征点的mtype类型匹配点，若能正确找到表明此特征点有mtype类型的匹配点，则将其放入_matched数组 if( get_match( features + i, mtype ) ) { rdata = malloc( sizeof( struct ransac_data ) );//为ransac_data结构分配空间 memset( rdata, 0, sizeof( struct ransac_data ) );//清零 rdata->orig_feat_data = features[i].feature_data;//保存第i个特征点的feature_data域之前的值 _matched[m] = features + i;//放到_matched数组 _matched[m]->feature_data = rdata;//其feature_data域赋值为ransac_data类型数据的指针 m++;//_matched数组中元素个数 }} *matched = _matched;//输出参数赋值 return m;//返回值，元素个数}问题1：feature结构体里的feature_data在RANSAC算法里是什么？和ransac_data有什么关系？
答：在SIFT极值点检测中，是detection_data结构的指针；在k-d树搜索中，是bbf_data结构的指针；在RANSAC算法中，是ransac_data结构的指针。而在RANSAC算法里ransac_data包括两部分：
struct ransac_data
{
void* orig_feat_data; //保存此特征点的feature_data域的以前的值
int sampled; //标识位，值为1标识此特征点是否被选为样本
};
问题2：RANSAC算法：从样本集matched中随机抽选一个RANSAC样本(即一个4个特征点的数组)，放到样本变量sample中，四个点怎么随机选？
答：采用srand和rand()配合使用,而rand()在函数draw_ransac_sample中，使用x = rand() % n;产生随机下标，而把该点的feature_data成员的sampled （标志位）置为 1;表明此点已选，在for循环找的m（m=4）个点不能重合。
函数说明：srand函数是随机数发生器的初始化函数。原型：void srand(unsigned int seed);srand和rand()配合使用产生伪随机数序列。
参考：百度百科——
问题3：当前计算出的模型的错误概率p怎么计算？
答：由公式计算：p = pow( 1.0 - pow( in_frac, m ), k );初始为p=(1-0.25^4)^0 = 1
此公式在书P166（7-4），in_frac为公式中的w，m为N，为迭代次数
（2.2.1.1）get_matched_features代码及说明：
答：
/*根据给定的匹配类型，返回输入特征点feat的匹配点
参数：
feat：输入特征点
mtype：匹配类型，是FEATURE_FWD_MATCH，FEATURE_BCK_MATCH，FEATURE_MDL_MATCH之一
返回值：feat的匹配点的指针，若为空表示mtype参数有误
static __inline struct feature* get_match( struct feature* feat, int mtype )
{
//FEATURE_MDL_MATCH：表明feature结构中的mdl_match域是对应的匹配点
if( mtype == FEATURE_MDL_MATCH )
return feat->mdl_match;
//FEATURE_BCK_MATCH：表明feature结构中的bck_match域是对应的匹配点
if( mtype == FEATURE_BCK_MATCH )
return feat->bck_match;
//FEATURE_FWD_MATCH：表明feature结构中的fwd_match域是对应的匹配点
if( mtype == FEATURE_FWD_MATCH )
return feat->fwd_match;
return NULL;
}
（2.2.2）calc_min_inliers代码及说明：
答：
/*计算保证RANSAC最终计算出的转换矩阵错误的概率小于p_badxform所需的最小内点数目
参数：
n：推定的匹配点对的个数
m：计算模型所需的最小点对个数，初始宏定义值4
p_badsupp：概率，错误模型被一个匹配点对支持的概率，初始宏定义值0.1
p_badxform：概率，最终计算出的转换矩阵是错误的的概率，初始宏定义值0.01
返回值：保证RANSAC最终计算出的转换矩阵错误的概率小于p_badxform所需的最小内点数目
static int calc_min_inliers( int n, int m, double p_badsupp, double p_badxform )
{
//根据论文：Chum, O. and Matas, J. Matching with PROSAC -- Progressive Sample Consensus中的一个公式计算，但是不知道为什么这么计算！
double pi, sum;
int i, j;
for( j = m+1; j <= n; j++ )
{
sum = 0;
for( i = j; i <= n; i++ )
{
pi = ( i - m ) * log( p_badsupp ) + ( n - i + m ) * log( 1.0 - p_badsupp ) +
log_factorial( n - m ) - log_factorial( i - m ) -
log_factorial( n - i );
/*
* Last three terms above are equivalent to log( n-m choose i-m )
*/
sum += exp( pi );
}
if( sum < p_badxform )
break;
}
return j;
}
问题：论文：Chum, O. and Matas, J. Matching with PROSAC -- Progressive Sample Consensus中公式？代码如何计算？
答：公式如下：
代码中两边取对数了，具体看我的演算纸：
（2.2.2.1）log_factorial代码及说明：
答：
//计算n的阶乘的自然对数 log（n!）
static __inline double log_factorial( int n )
{
double f = 0;
int i;
for( i = 1; i <= n; i++ )
f += log( i );
return f;
}
具体看我的演算纸：
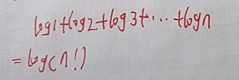
（2.2.3）draw_ransac_sample代码及说明：
答：
/*从给定的特征点集中随机抽选一个RANSAC样本(即一个4个特征点的数组)
参数：
features：作为样本集的特征点数组
n：features中元素个数
m：单个样本的尺寸，这里是4(至少需要4个点来计算变换矩阵)
返回值：一个指针数组，其元素指向被选为样本的特征点，被选为样本的特征点的feature_data域的sampled被设为1
static struct feature** draw_ransac_sample( struct feature** features, int n, int m )
{
struct feature** sample, * feat;//sample：被选为样本的点的数组
struct ransac_data* rdata;
int i, x;
//将所有特征点的feature_data域的sampled值都初始化为0，即未被选为样本点
for( i = 0; i < n; i++ )
{
//利用宏feat_ransac_data来提取参数中的feature_data成员并转换为ransac_data格式的指针
rdata = feat_ransac_data( features[i] );
rdata->sampled = 0;//sampled值设为0
}
sample = calloc( m, sizeof( struct feature* ) );//为样本数组分配空间
//随机抽取m个特征点作为一个样本，将其指针保存在sample数组中
for( i = 0; i < m; i++ )
{
do
{
x = rand() % n;//随机下标
feat = features[x];
rdata = feat_ransac_data( feat );//获得feature_data成员并转换为ransac_data格式的指针
}
while( rdata->sampled );//若抽取的特征点的sampled值为1，继续选取；否则停止，将其作为样本中的一个点
//sampled为标志位，初始为0，但（抽后边m-1次）之前已经抽过，为避免重复抽到，这样保证抽到了相异的四个点
sample[i] = feat;//放入sample数组
rdata->sampled = 1;//该点的feature_data成员的sampled域值设为1
}
return sample;//返回随机选取的样本
}
问题1：如何保证抽到的四个点随机且不同？
答：随机通过 srand和rand()函数配合使用，不同，通过标志位sampled
（2.2.4）extract_corresp_pts代码及说明：
答：
/*从特征点数组中获取特征点和其对应匹配点的二维坐标，分别放到输出参数pts和mpts中
参数：
features：特征点数组，将从其中抽取坐标点和其匹配点，此数组中所有特征点都应具有mtype类型的匹配点
n：feantures中特征点个数，n=4
mtype：匹配类型，若是FEATURE_MDL_MATCH，对应的匹配点对坐标是每个特征点的img_pt域和其匹配点的mdl_pt域， 否则，对应的匹配点对是每个特征点的img_pt域和其匹配点的img_pt域。三者之一
pts：输出参数，从特征点数组features中获取的二维坐标数组
mpts：输出参数，从特征点数组features的对应匹配点中获取的二维坐标数组
static void extract_corresp_pts( struct feature** features, int n, int mtype,
CvPoint2D64f** pts, CvPoint2D64f** mpts )
{
struct feature* match;//每个特征点对应的匹配点
CvPoint2D64f* _pts, * _mpts;
int i;
_pts = calloc( n, sizeof( CvPoint2D64f ) );//特征点的坐标数组，分配空间
_mpts = calloc( n, sizeof( CvPoint2D64f ) );//对应匹配点的坐标数组，发配空间
//匹配类型是FEATURE_MDL_MATCH，匹配点的坐标是mdl_pt域
if( mtype == FEATURE_MDL_MATCH )
for( i = 0; i < n; i++ )
{
//根据给定的匹配类型，返回输入特征点的匹配点
match = get_match( features[i], mtype );
if( ! match )
fatal_error( "feature does not have match of type %d, %s line %d",
mtype, __FILE__, __LINE__ );
_pts[i] = features[i]->img_pt;//特征点的坐标
_mpts[i] = match->mdl_pt;//对应匹配点的坐标
}
//匹配类型不是FEATURE_MDL_MATCH，匹配点的坐标是img_pt域
else
for( i = 0; i < n; i++ )
{
//根据给定的匹配类型，返回输入特征点的匹配点
match = get_match( features[i], mtype );
if( ! match )
fatal_error( "feature does not have match of type %d, %s line %d",
mtype, __FILE__, __LINE__ );
_pts[i] = features[i]->img_pt;//特征点的坐标
_mpts[i] = match->img_pt;//对应匹配点的坐标
}
*pts = _pts;
*mpts = _mpts;
}
（2.2.5）xform_fn，一般传入lsq_homog()函数代码及说明：
答：
/* 根据4对坐标点计算最小二乘平面单应性变换矩阵
参数：
pts：坐标点数组
mpts：对应点数组，pts[i]与mpts[i]一一对应
n：pts和mpts数组中点的个数，pts和mpts中点的个数必须相同，一般是4
返回值：一个3*3的变换矩阵，将pts中的每一个点转换为mpts中的对应点，返回值为空表示失败
CvMat* lsq_homog( CvPoint2D64f* pts, CvPoint2D64f* mpts, int n )
{
CvMat* H, * A, * B, X;
double x[9];//数组x中的元素就是变换矩阵H中的值
int i;
//输入点对个数不够4
if( n < 4 )
{
fprintf( stderr, "Warning: too few points in lsq_homog(), %s line %d\n",
__FILE__, __LINE__ );
return NULL;
}
//将变换矩阵H展开到一个8维列向量X中，使得AX=B，这样只需一次解线性方程组即可求出X，然后再根据X恢复H
/* set up matrices so we can unstack homography into X; AX = B */
A = cvCreateMat( 2*n, 8, CV_64FC1 );//创建2n*8的矩阵，一般是8*8
B = cvCreateMat( 2*n, 1, CV_64FC1 );//创建2n*1的矩阵，一般是8*1
X = cvMat( 8, 1, CV_64FC1, x );//创建8*1的矩阵，指定数据为x
H = cvCreateMat(3, 3, CV_64FC1);//创建3*3的矩阵
cvZero( A );//将A清零
//由于是展开计算，需要根据原来的矩阵计算法则重新分配矩阵A和B的值的排列
for( i = 0; i < n; i++ )
{
cvmSet( A, i, 0, pts[i].x );//设置矩阵A的i行0列的值为pts[i].x
cvmSet( A, i+n, 3, pts[i].x );
cvmSet( A, i, 1, pts[i].y );
cvmSet( A, i+n, 4, pts[i].y );
cvmSet( A, i, 2, 1.0 );
cvmSet( A, i+n, 5, 1.0 );
cvmSet( A, i, 6, -pts[i].x * mpts[i].x );
cvmSet( A, i, 7, -pts[i].y * mpts[i].x );
cvmSet( A, i+n, 6, -pts[i].x * mpts[i].y );
cvmSet( A, i+n, 7, -pts[i].y * mpts[i].y );
cvmSet( B, i, 0, mpts[i].x );
cvmSet( B, i+n, 0, mpts[i].y );
}
//调用OpenCV函数，解线性方程组
cvSolve( A, B, &X, CV_SVD );//求X，使得AX=B
x[8] = 1.0;//变换矩阵的[3][3]位置的值为固定值1
X = cvMat( 3, 3, CV_64FC1, x );
cvConvert( &X, H );//将数组转换为矩阵
cvReleaseMat( &A );
cvReleaseMat( &B );
return H;
}
问题1：cvMat函数？X = cvMat( 8, 1, CV_64FC1, x );//创建8*1的矩阵，指定数据为x？
答：
初始化矩阵:
double a[] = { 1, 2, 3, 4,5, 6, 7, 8, 9, 10, 11, 12 };CvMat Ma=cvMat(3, 4, CV_64FC1, a);参看：1.opencv中矩阵计算的一些函数：2.CvMat用法详解：
问题2：四个点计算单应性变换矩阵？AX = B中A和B如何构建？
答：在齐次坐标中，假设一点p(xi,yi,1)经过H矩阵的变换变为p‘(xi',yi',1)，即 p' = H*p，通常，对于透视变换，H矩阵有8个自由度，这样至少需要4对特征点对求解。4个特征点对可以建立8个方程。那么对于有n对特征点的情况(超定方程)，解p' = H*p方程组可以转化为对齐次方程组Ax = 0 的求解。而对 Ax = 0 的求解转化为 min ||Ax||2 的非线性优化问题（超定方程，通过最小二乘拟合得到近似解）。
对于某一点(xi,yi)，其变换可表述为 p' = H*p，代入展开可得：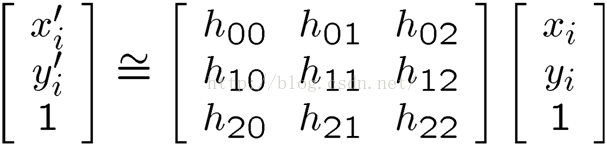
(1) 那么可得：
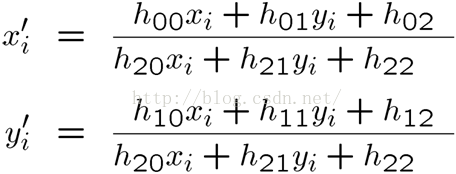(2)
进一步变换为：
(3)这样便可构造系数矩阵：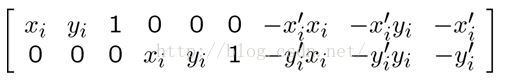
(4)通过系数矩阵我们可以构造出齐次线性方程组(Ax = 0)： 
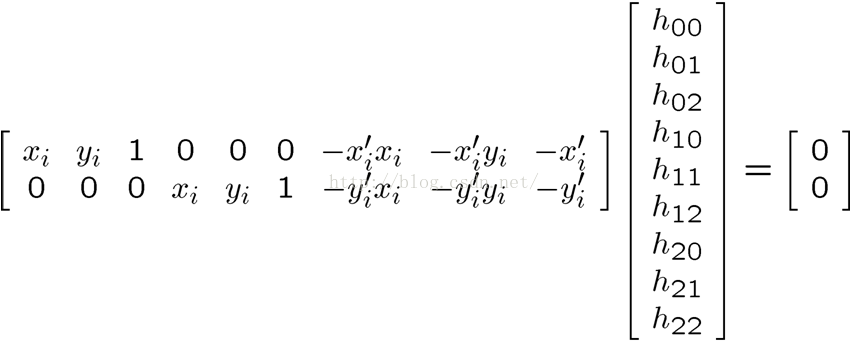(5)
即：
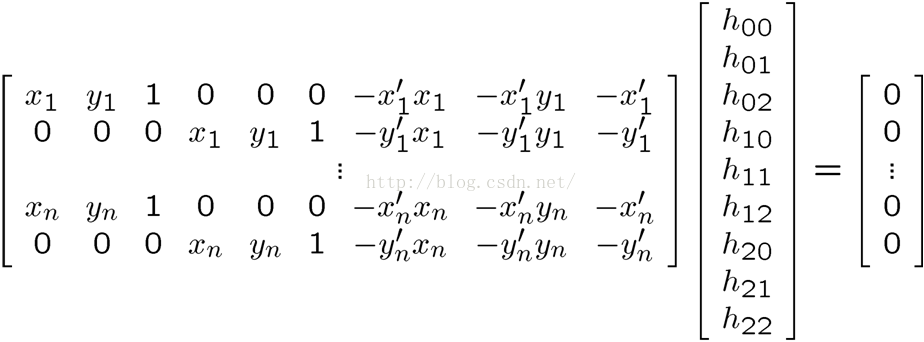(6)
对于(6)这样的超定方程求解，可以通过最小二乘的方式求解。通过对系数矩阵A求取特征值和特征向量得到。通过以下方式获得最小二乘解：[V,D] = eig(A'*A) (7)其中D是特征值对角矩阵(特征值沿主对角线降序)，V是对应D特征值的特征向量(列向量)组成的特征矩阵,A'表示A的转置。其最小二乘解为V(1)，即系数矩阵A最小特征值对应的特征向量就是超定方程组Ax = 0的最小二乘解。至此，H矩阵已经求取，后续可以通过随机采样一致性(RANSC)进行精选，或者通过LM进行优化。
参看：原理参看：四点求解单应性矩阵：
结果参看：特征点匹配——使用基础矩阵、单应性矩阵的RANSAC算法去除误匹配点对：
问题3：计算了单应性变换矩阵H后如何使用？
答：每次从所有的匹配点中选出4对，计算单应性矩阵H，然后选出内点个数最多的作为最终的结果。计算距离方法如下：
参看：特征点匹配——使用基础矩阵、单应性矩阵的RANSAC算法去除误匹配点对：
（2.2.6）find_consensus代码及说明：
答：
/*对于给定的模型和错误度量函数，从特征点集和中找出一致集
参数：
features：特征点集合，其中的特征点都具有mtype类型的匹配点
n：特征点的个数
mtype：匹配类型，若是FEATURE_MDL_MATCH，对应的匹配点对坐标是每个特征点的img_pt域和其匹配点的mdl_pt域，否则，对应的匹配点对是每个特征点的img_pt域和其匹配点的img_pt域。
M：给定的模型，即一个变换矩阵
err_fn：错误度量函数，对于给定的变换矩阵，计算推定的匹配点对之间的变换误差
err_tol：容错度，用来衡量err_fn的返回值，小于err_tol的被加入一致集
consensus：输出参数，一致集，即一致集中特征点构成的数组
返回值：一致集中特征点的个数
static int find_consensus( struct feature** features, int n, int mtype,
CvMat* M, ransac_err_fn err_fn, double err_tol,
struct feature*** consensus )
{
struct feature** _consensus;//一致集
struct feature* match;//每个特征点对应的匹配点
CvPoint2D64f pt, mpt;//pt:当前特征点的坐标，mpt：当前特征点的匹配点的坐标
double err;//变换误差
int i, in = 0;
_consensus = calloc( n, sizeof( struct feature* ) );//给一致集分配空间
//匹配类型是FEATURE_MDL_MATCH，匹配点的坐标是mdl_pt域
if( mtype == FEATURE_MDL_MATCH )
for( i = 0; i < n; i++ )
{
//根据给定的匹配类型，返回输入特征点的匹配点
match = get_match( features[i], mtype );
if( ! match )
fatal_error( "feature does not have match of type %d, %s line %d",
mtype, __FILE__, __LINE__ );
pt = features[i]->img_pt;//特征点的坐标
mpt = match->mdl_pt;//对应匹配点的坐标
err = err_fn( pt, mpt, M );//计算"pt经M变换后的点"和mpt之间的距离的平方，即变换误差
if( err <= err_tol )//若变换误差小于容错度，将其加入一致集
_consensus[in++] = features[i];
}
//匹配类型不是FEATURE_MDL_MATCH，匹配点的坐标是img_pt域
else
for( i = 0; i < n; i++ )
{
//根据给定的匹配类型，返回输入特征点的匹配点
match = get_match( features[i], mtype );
if( ! match )
fatal_error( "feature does not have match of type %d, %s line %d",
mtype, __FILE__, __LINE__ );
pt = features[i]->img_pt;//特征点的坐标
mpt = match->img_pt;//对应匹配点的坐标
err = err_fn( pt, mpt, M );//计算"pt经M变换后的点"和mpt之间的距离的平方，即变换误差
if( err <= err_tol )//若变换误差小于容错度，将其加入一致集
_consensus[in++] = features[i];
}
*consensus = _consensus;
return in;//返回一致集中元素个数
}
（2.2.6.1）homog_xfer_err代码及说明：
答：
/*对于给定的单应性矩阵H，计算输入点pt精H变换后的点与其匹配点mpt之间的误差
例如：给定点x，其对应点x'，单应性矩阵H，则计算x'与Hx之间的距离的平方，d(x', Hx)^2
参数：
pt：一个点
mpt：pt的对应匹配点
H：单应性矩阵
返回值：转换误差
*/
double homog_xfer_err( CvPoint2D64f pt, CvPoint2D64f mpt, CvMat* H )
{
CvPoint2D64f xpt = persp_xform_pt( pt, H );//pt经变换矩阵H变换后的点xpt,即H乘以x对应的向量
return sqrt( dist_sq_2D( xpt, mpt ) );//两点间距离的平方
}
（2.2.6.1.1）persp_xform_pt代码及说明：
答：
/*计算点pt经透视变换后的点，即给定一点pt和透视变换矩阵T，计算变换后的点
给定点(x,y)，变换矩阵M，计算[x',y',w']^T = M * [x,y,1]^T(^T表示转置)，
则变换后的点是(u,v) = (x'/w', y'/w')
注意：仿射变换是透视变换的特例
参数：
pt：一个二维点
T：透视变换矩阵
返回值：pt经透视变换后的点
*/
CvPoint2D64f persp_xform_pt( CvPoint2D64f pt, CvMat* T )
{
//XY：点pt对应的3*1列向量，UV：pt变换后的点对应的3*1列向量
CvMat XY, UV;
double xy[3] = { pt.x, pt.y, 1.0 }, uv[3] = { 0 };//对应的数据
CvPoint2D64f rslt;//结果
//初始化矩阵头
cvInitMatHeader( &XY, 3, 1, CV_64FC1, xy, CV_AUTOSTEP );
cvInitMatHeader( &UV, 3, 1, CV_64FC1, uv, CV_AUTOSTEP );
cvMatMul( T, &XY, &UV );//计算矩阵乘法，T*XY,结果放在UV中
rslt = cvPoint2D64f( uv[0] / uv[2], uv[1] / uv[2] );//得到转换后的点
return rslt;
}
问题1：为什么要进行透视变换？公式是怎么样的？
答：透视变换能保持“直线性”，即原图像里面的直线，经透视变换后仍为直线。
透视变换矩阵变换公式为：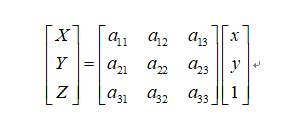
其中透视变换矩阵：
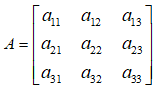要移动的点，即源目标点为：
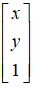另外定点，即移动到的目标点为：
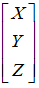这是一个从二维空间变换到三维空间的转换，因为图像在二维平面，故除以Z， （X';Y';Z'）表示图像上的点：
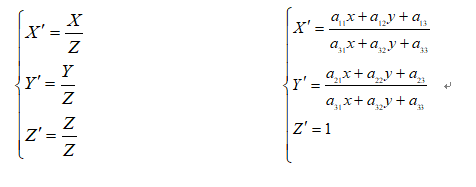令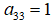
，展开上面公式，得到一个点的情况：
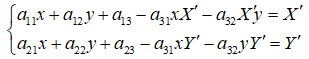
4个点可以得到8个方程，即可解出A。
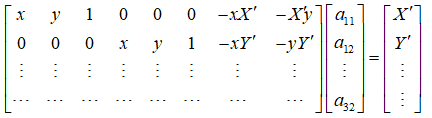
参看：图像透视变换原理及实现——
问题2：cvMatMul函数怎么使用？
答：#define cvMatMul(src1,src2,dst); 表示dst=src1*src2
参看：cvGEMM、cvMatMul和cvMatMulAdd的定义——
（2.2.6.1.2）dist_sq_2D代码及说明：
答：
//计算两点之间距离的平方
double dist_sq_2D( CvPoint2D64f p1, CvPoint2D64f p2 )
{
double x_diff = p1.x - p2.x;
double y_diff = p1.y - p2.y;
return x_diff * x_diff + y_diff * y_diff; //(x1-x2)^2+(y1-y2)^2
}
问题：如何计算两点间的距离——欧式距离？
参看：百度百科（欧几里得度量）——
（2.2.6）release_mem代码及说明：
答：
/*释放输入参数的存储空间
static __inline void release_mem( CvPoint2D64f* pts1, CvPoint2D64f* pts2,
struct feature** features )
{
free( pts1 );
free( pts2 );
if( features )
free( features );
}
（2.2.7）extract_corresp_pts代码及说明：
答：
/*从特征点数组中获取特征点和其对应匹配点的二维坐标，分别放到输出参数pts和mpts中
参数：
features：特征点数组，将从其中抽取坐标点和其匹配点，此数组中所有特征点都应具有mtype类型的匹配点
n：feantures中特征点个数，n=4
mtype：匹配类型，若是FEATURE_MDL_MATCH，对应的匹配点对坐标是每个特征点的img_pt域和其匹配点的mdl_pt域，否则，对应的匹配点对是每个特征点的img_pt域和其匹配点的img_pt域。三者之一
pts：输出参数，从特征点数组features中获取的二维坐标数组
mpts：输出参数，从特征点数组features的对应匹配点中获取的二维坐标数组
static void extract_corresp_pts( struct feature** features, int n, int mtype,
CvPoint2D64f** pts, CvPoint2D64f** mpts )
{
struct feature* match;//每个特征点对应的匹配点
CvPoint2D64f* _pts, * _mpts;
int i;
_pts = calloc( n, sizeof( CvPoint2D64f ) );//特征点的坐标数组
_mpts = calloc( n, sizeof( CvPoint2D64f ) );//对应匹配点的坐标数组
//匹配类型是FEATURE_MDL_MATCH，匹配点的坐标是mdl_pt域
if( mtype == FEATURE_MDL_MATCH )
for( i = 0; i < n; i++ )
{
//根据给定的匹配类型，返回输入特征点的匹配点
match = get_match( features[i], mtype );
if( ! match )
fatal_error( "feature does not have match of type %d, %s line %d",
mtype, __FILE__, __LINE__ );
_pts[i] = features[i]->img_pt;//特征点的坐标
_mpts[i] = match->mdl_pt;//对应匹配点的坐标
}
//匹配类型不是FEATURE_MDL_MATCH，匹配点的坐标是img_pt域
else
for( i = 0; i < n; i++ )
{
//根据给定的匹配类型，返回输入特征点的匹配点
match = get_match( features[i], mtype );
if( ! match )
fatal_error( "feature does not have match of type %d, %s line %d",
mtype, __FILE__, __LINE__ );
_pts[i] = features[i]->img_pt;//特征点的坐标
_mpts[i] = match->img_pt;//对应匹配点的坐标
}
*pts = _pts;
*mpts = _mpts;
}
（2.3）cvWarpPerspective函数说明：
答：
说明：密集透视变换
参看：1）第六章 - 图像变换 - 图像拉伸、收缩、扭曲、旋转[2] - 透视变换(cvWarpPerspective)——
2）【OpenCV3】透视变换——cv::getPerspectiveTransform()与cv::warpPerspective()详解——
附：
1.CvPoint函数说明？参看：opencv的基本数据类型CvPoint，CvSize，CvRect和CvScalar——